Application examples

We use the framework discussed in paper I as the baseline for the line transfer problems discussed in this paper. In addition to the highly efficient parallelization of solid angle space, we have implemented a parallelization over wavelength space using the MPI distributed memory model. For static configurations (or for configurations with velocity fields treated in the Eulerian frame) there is no direct coupling between different wavelength points.

Our basic setup is similar to that discussed in paper I. We use a sphere with a grey continuum opacity parameterized by a power law in the continuum optical depth $\ifmmode{\tau_{\rm std}}\else\hbox{$\tau_{\rm std}$}\fi$. The basic model parameters are

1. Inner radius $r_c=10^{13}\,$cm, outer radius $\hbox{$r_{\rm out}$} = 1.01\times 10^{15}\,$cm.
2. Minimum optical depth in the continuum $\tau _{\rm std}^{\rm min} = 10^{-4}$ and maximum optical depth in the continuum $\tau _{\rm std}^{\rm max} = 1$.
3. constant temperature structure with $T=10^4$ K or
4. grey temperature structure with $\hbox{$\,T_{\rm eff}$} =10^4$ K.
5. Outer boundary condition $I_{\rm bc}^{-} \equiv 0$ and diffusion inner boundary condition for all wavelengths.
6. Continuum extinction $\chi_c = C/r^2$, with the constant $C$ fixed by the radius and optical depth grids.
7. Parameterized coherent & isotropic continuum scattering by defining
   
   $$\chi_c = \epsilon_c \kappa_c + (1-\epsilon_c) \sigma_c$$
   
   
   with $0\le \epsilon_c \le 1$. $\kappa_c$ and $\sigma_c$ are the continuum absorption and scattering coefficients.

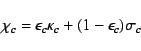
The line of the simple 2-level model atom is parameterized by the ratio of the profile averaged line opacity $\chi_l$ to the continuum opacity $\chi_c$ and the line thermalization parameter $\epsilon _l$. For the test cases presented below, we have used $\epsilon_c=1$ and a constant temperature and thus a constant thermal part of the source function for simplicity (and to save computing time) and set $\chi_l/\chi_c = 10^6$ to simulate a strong line, with varying $\epsilon _l$ (see below). With this setup, the optical depths as seen in the line range from $10^{-2}$ to $10^6$. We use 32 wavelength points to model the full line profile, including wavelengths outside the line for the continuum. We did not require the line to thermalize at the center of the test configurations, this is a typical situation one encounters in a full 3D configurations as the location (or even existence) of the thermalization depths becomes more ambiguous than in the 1D case.

The sphere is put at the center of the Cartesian grid, which is in each axis 10% larger than the radius of the sphere. For the test calculations we use voxel grids with the same number of spatial points in each direction (see below). The solid angle space was discretized in $(\theta,\phi)$ with $n_\theta=n_\phi$ if not stated otherwise. In the following we discuss the results of various tests. In all tests we use the LC method for the 3D RT solution. Unless otherwise stated, the tests were run on parallel computers using 128 CPUs. For the 3D solver we use $n_x=n_y=n_z=2*64+1$ or $n_x=n_y=n_z=2*96+1$ points along each axis, for a total of $129^3$ or $193^3$ spatial points, depending on the test case. The solid angle space discretization uses $n_\theta=n_\phi=64$ points.