For a diagonal
![]() the solution of Eq. 6 is just a division by
the solution of Eq. 6 is just a division by
![]() which requires very little effort. For the
non-local
which requires very little effort. For the
non-local
![]() operator, a matrix equation has to be solved at each step in
order to compute
operator, a matrix equation has to be solved at each step in
order to compute
![]() . For the nearest neighbor operator the matrix
structure is that of a sparse band matrix where the bandwidth of the matrix is
proportional to the square of the maximum number of points along a coordinate
and there are a total of 27 non-zero entries in every column of the matrix.
This system can be solved by any suitable method. For example, we have
implemented a solver based on LAPACK (Anderson et al., 1992) routines. Although this solver works
fine for small grids [
. For the nearest neighbor operator the matrix
structure is that of a sparse band matrix where the bandwidth of the matrix is
proportional to the square of the maximum number of points along a coordinate
and there are a total of 27 non-zero entries in every column of the matrix.
This system can be solved by any suitable method. For example, we have
implemented a solver based on LAPACK (Anderson et al., 1992) routines. Although this solver works
fine for small grids [![]() voxels with a bandwidth of 1123], the memory
requirements rise beyond available single-CPU limits with already only
voxels with a bandwidth of 1123], the memory
requirements rise beyond available single-CPU limits with already only ![]() voxels
with a bandwidth of 4291. For a more realistic grid of
voxels
with a bandwidth of 4291. For a more realistic grid of ![]() voxels the
bandwidth is more than 250,000. Therefore, a standard band matrix solver is
only useful for comparison and testing on very small grids. Other sparse
matrix solvers (for example, Xiaoye & Demmel, 2003) have similar memory
scaling properties.
voxels the
bandwidth is more than 250,000. Therefore, a standard band matrix solver is
only useful for comparison and testing on very small grids. Other sparse
matrix solvers (for example, Xiaoye & Demmel, 2003) have similar memory
scaling properties.
As an alternative to direct solutions of Eq. 6 we have implemented
iterative solvers. These solvers have the huge advantage that their
memory requirements are minimal to modest. In addition, they can be
tailored to the special format of the matrix in Eq. 6 which makes
coding the methods very simple.
We obtained extremely good results with
the Jordan and the Gauss-Seidel methods, which converge rapidly to a
relative accuracy of ![]() . For either method, Ng acceleration
turned out to be very useful, reducing the number of iterations significantly.
In addition, the Rapido method (Zurmühl & Falk, 1986) which was constructed to solve
systems of the form
. For either method, Ng acceleration
turned out to be very useful, reducing the number of iterations significantly.
In addition, the Rapido method (Zurmühl & Falk, 1986) which was constructed to solve
systems of the form
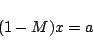 |
(27) |