

Next: About this document ...
Up: A 3D radiative transfer
Previous: Conclusions
-
Adam, J. 1990, A&A, 240, 541
-
-
Anderson, E., Bai, Z., Bischof, C., et al. 1992, LAPACK Users' Guide (SIAM)
-
-
Auer, L. 2003, in Stellar Atmosphere Modeling, ed. I. Hubeny, D. Mihalas, &
K. Werner, Vol. 288 (San Franscisco: ASP Conf. Series), 3
-
-
Auer, L., Fabiani Bendicho, P., & Trujillo Bueno, J. 1994, A&A, 292,
599
-
-
Cannon, C. J. 1973, JQSRT, 13, 627
-
-
Dykema, P. G., Klein, R. I., & Castor, J. I. 1996, ApJ, 457, 892
-
-
Fabiani Bendicho, P., Trujillo Bueno, J., & Auer, L. 1997, A&A, 324,
161
-
-
Golub, G. H. & Van Loan, C. F. 1989, Matrix computations (Baltimore: Johns
Hopkins University Press)
-
-
Hamann, W.-R. 1987, in Numerical Radiative Transfer, ed. W. Kalkofen (Cambridge
University Press), 35
-
-
Hauschildt, P. H. 1992, JQSRT, 47, 433
-
-
Hauschildt, P. H. & Baron, E. 2004, , 417, 317
-
-
Hauschildt, P. H., Störzer, H., & Baron, E. 1994, JQSRT, 51, 875
-
-
Hummel, W. 1994a, Astrophys. Space. Sci., 216, 87
-
-
Hummel, W. 1994b, A&A, 289, 458
-
-
Hummel, W. & Dachs, J. 1992, A&A, 262, L17
-
-
Mihalas, D. 1978, Stellar Atmospheres (New York: W. H. Freeman)
-
-
Mihalas, D. 1980, ApJ, 237, 574
-
-
Mihalas, D., Kunasz, P., & Hummer, D. 1975, ApJ, 202, 465
-
-
Ng, K. C. 1974, J. Chem. Phys., 61, 2680
-
-
Norman, M. L. 2000, in Revista Mexicana de Astronomia y Astrofisica
Conference Series, Vol. 9, 66-71
-
-
Olson, G. L., Auer, L. H., & Buchler, J. R. 1987, JQSRT, 38, 431
-
-
Olson, G. L. & Kunasz, P. B. 1987, JQSRT, 38, 325
-
-
Papkalla, R. 1995, A&A, 295, 551
-
-
Rijkhorst, E.-J., Plewa, T., Dubey, A., & Mellema, G. 2005, A&A, in press,
astro-ph/0505213
-
-
Steiner, O. 1991, A&A, 242, 290
-
-
Trujillo Bueno, J. & Fabiani Bendicho, P. 1995, ApJ, 455, 646
-
-
Turek, S. 1993, preprint
-
-
van Noort, M., Hubeny, I., & Lanz, T. 2002, ApJ, 568, 1066
-
-
Vath, H. M. 1994, A&A, 284, 319
-
-
Xiaoye, S. L. & Demmel, J. W. 2003, ACM Transaction on Mathematical Software,
29, 110
-
-
Zurmühl, R. & Falk, S. 1986, Matrizen und ihre Anwendungen, 5th edn.,
Vol. 2 (Berlin: Springer-Verlag)
-
Figure 1:
Schematic sketch of the different
types of characteristics used in the framework. The left panel
shows the long characteristics, the right panel the short characteristics.
The voxel boundaries and centers ('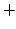 ' symbols) are indicated.
The '
' symbols) are indicated.
The '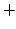 ' denote the points between which the geometric distance
is used to compute optical depth steps.
' denote the points between which the geometric distance
is used to compute optical depth steps.
|
Figure 2:
Comparison of the results obtained
for the LTE test with the 1D solver (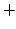 symbols) and the 3D solver.
The
symbols) and the 3D solver.
The 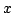 axis shows the distances from the center of the sphere, the
axis shows the distances from the center of the sphere, the
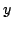 axis the
axis the 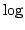 of the mean intensity.
of the mean intensity.
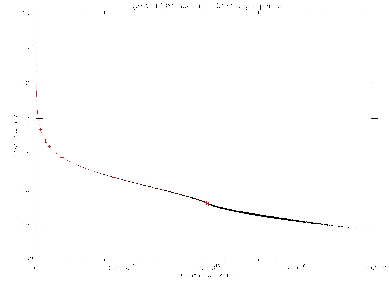 |
Figure 3:
Comparison of the results obtained
for the scattering dominated (
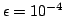 ) test with the 1D solver (
) test with the 1D solver (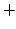 symbols) and the 3D solver.
The
symbols) and the 3D solver.
The 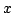 axis shows the distances from the center of the sphere, the
axis shows the distances from the center of the sphere, the
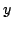 axis the
axis the 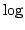 of the mean intensity. The top panel shows the
results for a (spatial; solid angle) grid with
of the mean intensity. The top panel shows the
results for a (spatial; solid angle) grid with 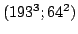 points, the middle panel
for
points, the middle panel
for 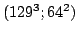 points and the bottom panel for
points and the bottom panel for  points.
points.
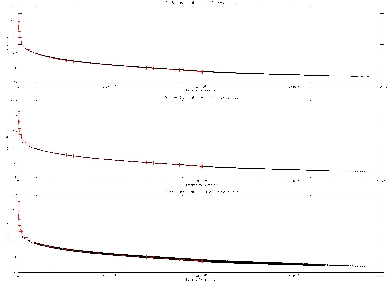 |
Figure 6:
Mean intensity surface at the
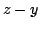 face for the test case
with
face for the test case
with
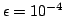 with
with 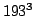 spatial points and
spatial points and
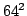 solid angle points. The axes are labeled
by voxel index with
solid angle points. The axes are labeled
by voxel index with
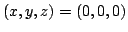 being the center of the
voxel grid.
being the center of the
voxel grid.
 |
Figure 7:
Convergence properties
of the codes for the
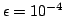 test case. The labels
indicate the different methods used. The 3D test runs use
test case. The labels
indicate the different methods used. The 3D test runs use
 spatial and
spatial and 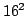 angular points.
angular points.
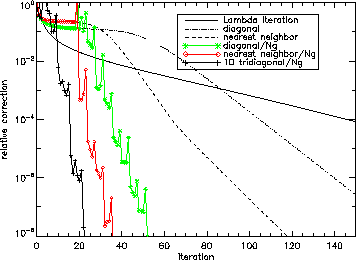 |
Figure 8:
Convergence properties
of the codes for the
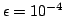 test case and different grid sizes. The labels
indicate the different grid sizes used, all but the
test case and different grid sizes. The labels
indicate the different grid sizes used, all but the  iteration use
the nearest neighbor operator with Ng acceleration.
iteration use
the nearest neighbor operator with Ng acceleration.
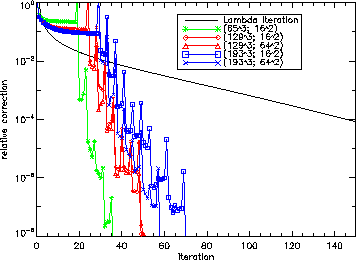 |
Figure 9:
Convergence properties of the
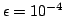 test case for various
test case for various
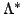 operator bandwidth choices with and without
Ng acceleration.
operator bandwidth choices with and without
Ng acceleration.
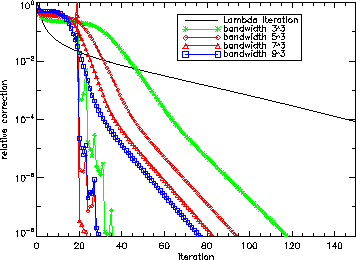 |
Figure 10:
Comparison of the results obtained
for the scattering dominated (
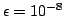 ) test with the 1D solver (
) test with the 1D solver (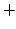 symbols) and the 3D solver.
The
symbols) and the 3D solver.
The 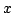 axis shows the distances from the center of the sphere, the
axis shows the distances from the center of the sphere, the
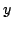 axis the
axis the 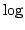 of the mean intensity. The graph shows the
results for a (spatial; solid angle) grid with
of the mean intensity. The graph shows the
results for a (spatial; solid angle) grid with 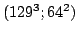 points. Note
the large dynamic range (12 dex) of the mean intensities.
points. Note
the large dynamic range (12 dex) of the mean intensities.
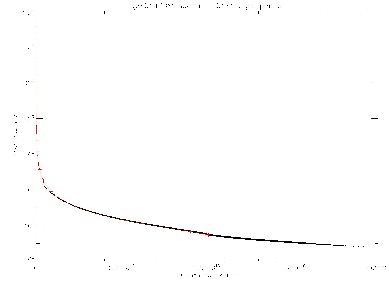 |
Figure 11:
Comparison of the results obtained
for the scattering dominated (
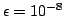 ) test with the 1D solver (
) test with the 1D solver (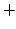 symbols) and the 3D solver
for slices along the
symbols) and the 3D solver
for slices along the 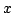 ,
, 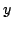 , and
, and 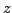 axes.
The plot shows the
results for a (spatial; solid angle) grid with
axes.
The plot shows the
results for a (spatial; solid angle) grid with 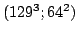 points. Note
the large dynamic range (12 dex) of the mean intensities.
points. Note
the large dynamic range (12 dex) of the mean intensities.
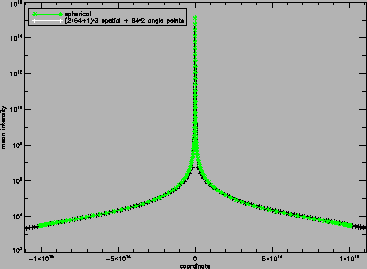 |
Figure 12:
Convergence properties
of the codes for the
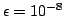 test case. The labels
indicate the different methods used. These test runs use
test case. The labels
indicate the different methods used. These test runs use
 spatial and
spatial and 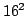 angular points.
angular points.
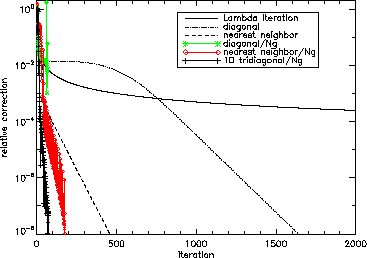 |
Figure 13:
Convergence properties
of the codes for the
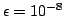 test case and different angular grid sizes. The labels
indicate the different grid sizes used, all but the
test case and different angular grid sizes. The labels
indicate the different grid sizes used, all but the  iteration use
the nearest neighbor operator with Ng acceleration.
iteration use
the nearest neighbor operator with Ng acceleration.
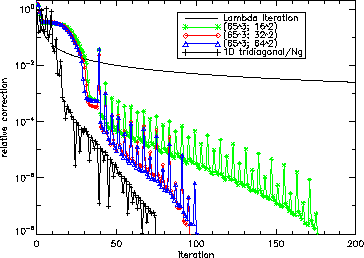 |
Figure 18:
Scaling properties of the MPI version
of the 3D RT code for parallel clusters based on Opterons and G5 CPUs.
In absolute scales the G5s are about 30% faster than the Opterons.
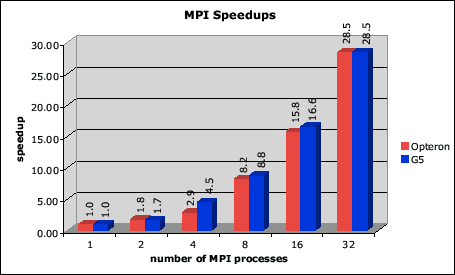 |
Figure 19:
Comparison of the mean intensity contour
plots for the test case with
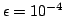 with
with  spatial points and
spatial points and
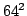 solid angle points. The left panel shows the results obtained with the
short characteristics method whereas the right panel shows the results of
the long characteristics method. The axes are labeled by
voxel index with
solid angle points. The left panel shows the results obtained with the
short characteristics method whereas the right panel shows the results of
the long characteristics method. The axes are labeled by
voxel index with
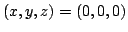 being the center of the voxel grid. Each
plot shows one outside face of the voxel cube (the physical scales are the same
an all directions).
being the center of the voxel grid. Each
plot shows one outside face of the voxel cube (the physical scales are the same
an all directions).
|


Next: About this document ...
Up: A 3D radiative transfer
Previous: Conclusions
Peter Hauschildt
2006-01-09










