As a first step we have implemented the method as a MPI parallelized Fortran 95 program. The parallelization of the formal solution is presently implemented over solid angle space as this is the simplest parallelization option and also one of the most efficient (a domain decomposition parallelization method will be discussed in a subsequent paper). In addition, the Jordan solver of the Operator splitting equations is parallelized with MPI (see below for scaling properties of the MPI implementation). The number of parallelization related statements in the code is small, about 320 out of a total of about 7900.
Our basic continuum scattering test problem is similar to that discussed in
Hauschildt (1992) and in Hauschildt & Baron (2004). This test problem covers a
large dynamic range of about 9 dex in the opacities and overall optical depth
steps along the characteristics and, in our experience, constitutes a
reasonably challenging setup for the radiative transfer code.The
application of the 3D code to 'real' problems is in preparation and requires a
substantial amount of development work (in progress). For the 1D code we have
found that the test case is actually pretty much a worst case scenario and that
it generally works better in real world problems. We use a sphere with a
grey continuum opacity parameterized by a power law in the continuum optical
depth
![]() . The basic model parameters are
. The basic model parameters are
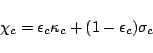 |
(28) |