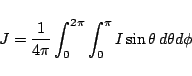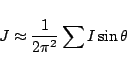

Next: Computation of
Up: Method
Previous: The operator splitting method
The formal solution through the voxel grid can be performed by a variety of
methods. So far, we have implemented both a short-characteristic
(SC, Olson et al., 1987) and a long-characteristic (LC) method. Long and
short characteristics are shown schematically in Fig. 1. In our
current implementation, the long characteristics are followed continuously
through the voxel grid, the short characteristics start at the center
of a voxel and step closest to the center of the next voxel. The distances
along a (short or long) characteristic are then used to compute the optical
depth steps. Along a characteristic (either short or long), the
formal solution is computed using a piece-wise parabolic (PPM) or piece-wise
linear (PLM) interpolation and integration of the source function
(Olson & Kunasz, 1987). Auer (2003) discusses the effect that high order interpolation
may cause problems, therefore, we automatically use piece-wise linear
interpolation if the change in the source function along the 3 points of the
PPM step would be larger than a prescribed threshold (typically factors of 100)
or if the optical depth along the characteristic is very small (typically less
than 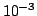 ). Depending on the direction
). Depending on the direction  of the
characteristic, the formal solution proceeds through the voxel grid.
of the
characteristic, the formal solution proceeds through the voxel grid.
Therefore, along a characteristic [which is in the static case just a straight
line with given  ] the transport equation is
simply
] the transport equation is
simply
 |
(8) |
With this definition,
the formal solution of the RTE along the characteristics can be written
in the following way (cf. Olson & Kunasz, 1987, for a derivation of
the formulae)
where we have suppressed the index labeling the characteristic; 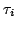 denotes the
optical depth along the characteristic with
denotes the
optical depth along the characteristic with
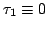 and
and
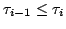 while
while 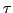 is calculated using piecewise linear interpolation of
is calculated using piecewise linear interpolation of
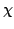 along the characteristic, viz.
along the characteristic, viz.
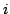 labels the points along a characteristic and
labels the points along a characteristic and
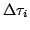 is calculated using piecewise linear interpolation of
is calculated using piecewise linear interpolation of 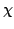 along the
characteristic
along the
characteristic
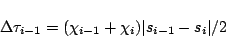 |
(11) |
The starting points
of each characteristic are
at the center of the voxels on their starting faces of the voxel grid.
The source function  along a characteristic is interpolated by
linear or parabolic polynomials so that
along a characteristic is interpolated by
linear or parabolic polynomials so that
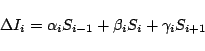 |
(12) |
with
for parabolic interpolation and
for linear interpolation.
The auxiliary functions are given by
and
 is the optical depth along the
characteristic from point
is the optical depth along the
characteristic from point 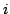 to point
to point 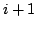 . The linear coefficients have to be used (at
least) at the last integration point along each characteristic, and for some
cases it might be
better to also use linear interpolation for some inner points so as to ensure
stability.
. The linear coefficients have to be used (at
least) at the last integration point along each characteristic, and for some
cases it might be
better to also use linear interpolation for some inner points so as to ensure
stability.
The integration over solid angle can be done in the static case using a simple
Simpson or trapezoidal quadrature formula. However, in the case of Lagrangian frame
radiation transport, the angles  vary along a (curved)
characteristic. Therefore, the
vary along a (curved)
characteristic. Therefore, the  grid changes for each voxel and
developing a quadrature formula in advance requires a pass through all voxels,
storing all
grid changes for each voxel and
developing a quadrature formula in advance requires a pass through all voxels,
storing all  points for each of them. For larger grids this will
amount to substantial long term memory requirements as the resulting quadrature
weights will have to be stored for each
points for each of them. For larger grids this will
amount to substantial long term memory requirements as the resulting quadrature
weights will have to be stored for each  pair at all voxels. To
avoid this, we have implemented a simple Monte-Carlo (MC) scheme to perform the
integration over solid angle.
In the MC integration, the integral
pair at all voxels. To
avoid this, we have implemented a simple Monte-Carlo (MC) scheme to perform the
integration over solid angle.
In the MC integration, the integral
is replaced by a simple MC sum of the form
where the sum goes over all solid angle points  .
The
.
The  are randomly selected and given equal weight in the MC
sums. This also works for precribed
are randomly selected and given equal weight in the MC
sums. This also works for precribed  grids as long as the
number of
grids as long as the
number of  points is sufficiently large. The accuracy is
improved by maintaining the normalization numerically for a unity valued test
function. The MC method has the advantage that the solid angle points can vary
from voxel to voxel (important for configurations with velocity fields where
the transfer equation is solved in the locally co-moving frame).
In the static case, the accuracy of the MC method
is only insignificantly worse than that of the deterministic quadrature,
which indicates that the MC integration will be very useful in
the case of 3D radiation transport in moving media.
points is sufficiently large. The accuracy is
improved by maintaining the normalization numerically for a unity valued test
function. The MC method has the advantage that the solid angle points can vary
from voxel to voxel (important for configurations with velocity fields where
the transfer equation is solved in the locally co-moving frame).
In the static case, the accuracy of the MC method
is only insignificantly worse than that of the deterministic quadrature,
which indicates that the MC integration will be very useful in
the case of 3D radiation transport in moving media.
Subsections


Next: Computation of
Up: Method
Previous: The operator splitting method
Peter Hauschildt
2006-01-09
![]() ). Depending on the direction
). Depending on the direction ![]() of the
characteristic, the formal solution proceeds through the voxel grid.
of the
characteristic, the formal solution proceeds through the voxel grid.
![]() ] the transport equation is
simply
] the transport equation is
simply

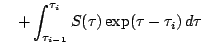
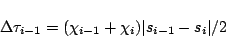
![]() along a characteristic is interpolated by
linear or parabolic polynomials so that
along a characteristic is interpolated by
linear or parabolic polynomials so that
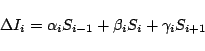
![]() vary along a (curved)
characteristic. Therefore, the
vary along a (curved)
characteristic. Therefore, the ![]() grid changes for each voxel and
developing a quadrature formula in advance requires a pass through all voxels,
storing all
grid changes for each voxel and
developing a quadrature formula in advance requires a pass through all voxels,
storing all ![]() points for each of them. For larger grids this will
amount to substantial long term memory requirements as the resulting quadrature
weights will have to be stored for each
points for each of them. For larger grids this will
amount to substantial long term memory requirements as the resulting quadrature
weights will have to be stored for each ![]() pair at all voxels. To
avoid this, we have implemented a simple Monte-Carlo (MC) scheme to perform the
integration over solid angle.
In the MC integration, the integral
pair at all voxels. To
avoid this, we have implemented a simple Monte-Carlo (MC) scheme to perform the
integration over solid angle.
In the MC integration, the integral