

Next: Computation of
Up: Radiative transfer in expanding
Previous: Radiative transfer in expanding
The idea of the ALI or operator splitting method is to reduce the
eigenvalues of the amplification matrix in the iteration scheme
[19] by
introducing an approximate 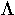 -operator (ALO)
-operator (ALO) 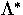 and to split
and to split 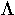 according to
according to
and rewrite Eq. 4 as
This relation can be written as [22]
where 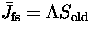 . Equation 8 is solved to get the new values of
. Equation 8 is solved to get the new values of
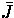 which is then used to compute the new
source function for the next iteration cycle.
which is then used to compute the new
source function for the next iteration cycle.
Mathematically, the ALI method belongs to the same family of iterative
methods as the Jacobi or the Gauss-Seidel methods
[28]. These
methods have the general form
for the iterative solution of a linear system Ax=b where the system
matrix A is split according to A=M-N. In the case of the ALI
method we have 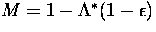 and, accordingly,
and, accordingly,
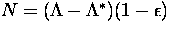 for the system matrix
for the system matrix 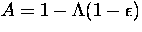 . The
convergence of the iterations depends on the spectral radius,
. The
convergence of the iterations depends on the spectral radius,
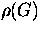 , of the iteration matrix G=M-1N. For convergence the
condition
, of the iteration matrix G=M-1N. For convergence the
condition 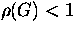 must be fulfilled, this puts a restriction on
the choice of
must be fulfilled, this puts a restriction on
the choice of 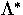 . In general, the iterations will converge
faster for a smaller spectral radius. To achieve a significant
improvement compared to the
. In general, the iterations will converge
faster for a smaller spectral radius. To achieve a significant
improvement compared to the 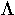 -iteration, the operator
-iteration, the operator 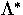 is
constructed so that the eigenvalues of the iteration matrix G are
much smaller than unity, resulting in swift convergence. Using
parts of the exact
is
constructed so that the eigenvalues of the iteration matrix G are
much smaller than unity, resulting in swift convergence. Using
parts of the exact 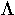 matrix (e.g., its diagonal or a tri-diagonal
form) will optimally reduce the eigenvalues of the
G. The
calculation and the structure of
matrix (e.g., its diagonal or a tri-diagonal
form) will optimally reduce the eigenvalues of the
G. The
calculation and the structure of 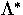 should be simple in order to
make the construction of the linear system in Eq. 8 fast. For
example, the choice
should be simple in order to
make the construction of the linear system in Eq. 8 fast. For
example, the choice 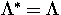 is best in view of the
convergence rate (it is equivalent to a direct solution by matrix inversion)
but the explicit construction of
is best in view of the
convergence rate (it is equivalent to a direct solution by matrix inversion)
but the explicit construction of 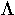 is more time
consuming than the construction of a simpler
is more time
consuming than the construction of a simpler 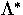 . The solution of
the system Eq. 8 in terms of linear algebra, using modern
linear algebra packages such as, e.g., LAPACK, is so fast that
its CPU time can be neglected for the small number of variables
encountered in 1D problems (typically the number of discrete shells
is about 50). However, for 2D or 3D problems the size of
. The solution of
the system Eq. 8 in terms of linear algebra, using modern
linear algebra packages such as, e.g., LAPACK, is so fast that
its CPU time can be neglected for the small number of variables
encountered in 1D problems (typically the number of discrete shells
is about 50). However, for 2D or 3D problems the size of 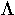 gets
very large due to the much larger number of grid points as compared to
the 1D case. Matrix inversions, which are necessary to solve
Eq. 8 directly, therefore become extremely time
consuming. This makes the direct solution of Eq. 8 more CPU intensive
even for
gets
very large due to the much larger number of grid points as compared to
the 1D case. Matrix inversions, which are necessary to solve
Eq. 8 directly, therefore become extremely time
consuming. This makes the direct solution of Eq. 8 more CPU intensive
even for 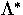 's of moderate bandwidth, except for the trivial case
of a diagonal
's of moderate bandwidth, except for the trivial case
of a diagonal 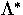 . Different methods like modified conjugate
gradient methods [29] may be effective for these
2D or 3D problems.
. Different methods like modified conjugate
gradient methods [29] may be effective for these
2D or 3D problems.
The CPU time required for the solution of the RTE using the ALI method depends
on several factors: (a) the time required for a formal solution and the
computation of 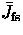 , (b) the time needed to construct
, (b) the time needed to construct 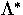 , (c) the time
required for the solution of Eq. 8, and (d) the number of iterations
required for convergence to the prescribed accuracy. Points (a), (b) and (c)
depend mostly on the number of discrete shells, and can be assumed to be fixed
for any given configuration. However, the number of iterations required to
convergence depends strongly on the bandwidth of
, (c) the time
required for the solution of Eq. 8, and (d) the number of iterations
required for convergence to the prescribed accuracy. Points (a), (b) and (c)
depend mostly on the number of discrete shells, and can be assumed to be fixed
for any given configuration. However, the number of iterations required to
convergence depends strongly on the bandwidth of 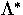 .This indicates, that there is an optimum
bandwidth of the
.This indicates, that there is an optimum
bandwidth of the 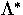 -operator which will result in the shortest possible
CPU time needed for the solution of the RTE, which we will discuss below.
-operator which will result in the shortest possible
CPU time needed for the solution of the RTE, which we will discuss below.


Next: Computation of
Up: Radiative transfer in expanding
Previous: Radiative transfer in expanding
Peter H. Hauschildt
8/20/1998
![]() -operator (ALO)
-operator (ALO) ![]() and to split
and to split ![]() according to
according to
![]() , (b) the time needed to construct
, (b) the time needed to construct ![]() , (c) the time
required for the solution of Eq. 8, and (d) the number of iterations
required for convergence to the prescribed accuracy. Points (a), (b) and (c)
depend mostly on the number of discrete shells, and can be assumed to be fixed
for any given configuration. However, the number of iterations required to
convergence depends strongly on the bandwidth of
, (c) the time
required for the solution of Eq. 8, and (d) the number of iterations
required for convergence to the prescribed accuracy. Points (a), (b) and (c)
depend mostly on the number of discrete shells, and can be assumed to be fixed
for any given configuration. However, the number of iterations required to
convergence depends strongly on the bandwidth of ![]() .This indicates, that there is an optimum
bandwidth of the
.This indicates, that there is an optimum
bandwidth of the ![]() -operator which will result in the shortest possible
CPU time needed for the solution of the RTE, which we will discuss below.
-operator which will result in the shortest possible
CPU time needed for the solution of the RTE, which we will discuss below.