Radiative transfer in expanding media

The equation of radiative transfer (RTE) in spherical symmetry for moving media has been solved with a number of different methods, e.g. Monte Carlo calculations [12,13,14], Sobolev methods [15], the tangent ray method [16], and the DOME method [17]. Only the tangent ray and the DOME method have been used to solve the RTE for very fast expanding shells (e.g. supernovae or novae) including the necessary special relativistic terms. Both methods need relatively large amounts of CPU time to compute the radiation field, mainly because of the need for matrix inversions (tangent ray method) or matrix diagonalization (DOME), which make both of them impractical for use within radiation-hydrodynamic studies of nova or supernova explosions. It has been shown [18] that the special relativistic terms in the RTE can be very important, even in the optically thick regions of expanding shells, and lead to results different than from the simpler approach which simply neglects the relativistic terms.

Recently, iterative methods for the solution of the RTE have been developed, based on the philosophy of operator perturbation [19,20]. Following these ideas, different approximate $\Lambda$-operators for this ``accelerated $\Lambda$-iteration'' (ALI) method have been used successfully [21,22,23] and have been applied to the construction of non-LTE, radiative equilibrium models of stellar atmospheres [23].

We describe the use of the short-characteristic method [21,24] to obtain the formal solution of the special relativistic, spherically symmetric radiative transfer equation (SSRTE) along its characteristic rays and then use a band-diagonal approximation to the discretized $\Lambda$-operator [1,24,25] as our choice of the approximate $\Lambda$-operator. This method can be implemented very efficiently to obtain an accurate solution of the SSRTE for continuum and line transfer problems using only modest amounts of computer resources.

The co-moving frame radiative transfer equation for spherically symmetric flows can be written as [26]:

$\beta=v/c$ is the velocity in units of the speed of light, c; and $\gamma = (1-\beta^2)^{-1/2}$ is the usual Lorentz factor. Equation 1 is a integro-differential equation, since the emissivity $\eta_\nu$ contains J_$J_{\nu}$ , the zeroth angular moment of I_$I_{\nu}$ :

$$\eta_\nu = \kappa_\nu \ifmmode{S_{\nu}}\else{\hbox{$S_{\nu}$... ...\fi +\sum_{\rm lines} \sigma_l(\nu) \int \phi_l J_\nu \,d\nu,$$

with

where $\ifmmode{S_{\nu}}\else{\hbox{$S_{\nu}$} }\fi$ is the source function, $\kappa_\nu$ is the absorption coefficient, $\sigma_\nu$ is the scattering coefficient for continuum processes, $\sigma_l$ are the line scattering coefficients, and $\phi_l$ is the line profile function. The independent variables are the radius r of the shell, the cosine $\mu$ of the angle between the radial direction and the propagation vector of the light (with $\mu=-1,1$ for radially inward and outward moving light, respectively), and the frequency $\nu=c/\lambda$ for a wavelength $\lambda$of the light. With the assumption of time-independence, $\frac{\partial\ifmmode{I_{\nu}}\else{\hbox{$I_{\nu}$} }\fi}{\partial t} = 0$, and a monotonic velocity field Eq. 1 becomes a boundary-value problem in the spatial coordinate and an initial value problem in the frequency or wavelength coordinate.

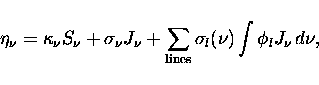
Switching from frequency to wavelength (Eq. 1 is presented in Ref. [1] in wavelength), the mean intensity $J_\lambda$ is obtained from the source function $S_\lambda$ by a formal solution of the RTE which is symbolically written using the $\Lambda$-operator $\Lambda_\lambda$ as  

$$J_\lambda = \Lambda_\lambda S_\lambda.$$ (1)

In the case of the transition of a two-level atom, we have

where $\bar J=\int \phi(\lambda) J_\lambda \,d\lambda$, $\Lambda=\int \phi(\lambda) \Lambda_\lambda \,d\lambda$ with the normalized line profile $\phi(\lambda)$. The line source function, for the simple case of a two-level atom without continuum and background absorption or scattering, is given by $S=(1-\epsilon){\bar J}+ \epsilon B$, where $\epsilon$ denotes the thermal coupling parameter and B is Planck's function.

The $\Lambda$-iteration method, i.e. to solve Eq. 4 by a fixed-point iteration scheme of the form

fails in the case of large optical depths and small $\epsilon$. This result is caused by the fact that the largest eigenvalue of the amplification matrix (in the case of Doppler-profiles) is approximately [16] $\lambda_{\rm max} \approx (1-\epsilon)(1-T^{-1})$, where T is the optical thickness of the medium. For small $\epsilon$ and large T, this is very close to unity and, therefore, the convergence rate of the $\Lambda$-iteration is very poor. A physical description of this effect can be found in Mihalas [27].