Condensation and the Chemical Equilibrium

The chemical equilibrium (hereafter CE) of the atmosphere code Phoenix already solves simultaneously for 40 elements with usually 2 to 6 ionization stages per element, and 600 molecular species relevant for oxygen-rich ideal gas compositions. This CE has been gradually updated since with additional molecular species using the polynomial partition functions by and . The molecular ions TiO⁺ and ZrO⁺, which have been found to be important in the balance of TiO and ZrO when departures from local thermodynamic equilibrium are present , have been added using the partition functions by . The ions H₃⁺ (and H₂⁺), which are important electron donors in low metallicity subdwarf stars and white dwarfs , has been added to our CE and opacity database by using the partition function by and a list of 3 million transitions by .

To include dust grains, we have expanded the system of CE to include the complete series of over 1000 liquids and crystals also studied by SH90. For each grain or liquid species, we followed the prescriptions of and used Gibbs free energy of formation $\Delta G(T)$, drawn from the JANAF 1986 database , to compute the so-called equilibrium pressures $P_{eq} = \exp^{-\Delta G(T)/RT}$ of the grains, where R is the gas constant and T the local gas temperature. P_eq was then compared to the pressure, P_c, obtained from the Guldberg law of mass-action (i.e. the product of the pressures of the constituting elements). The abundance of a condensed species was then determined by the condition that this species be in equilibrium with the gas phase, $P_c \ge P_{eq}$. For corundum,

$$P(Al_2O_3) = {P(Al)^2 P(O)^3 \over P_{eq}} P(Al_2O_3)^{max};$$

$$\quad for \,\, P_{eq} \le P(Al)^2 P(O)^3$$

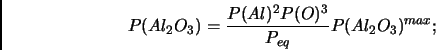
where max refers to the maximum concentration of grain cores (one core of corundum = one Al₂O₃ unit) given the conservation of the cores of each elements. The complete CE was then solved by Newton-Raphson iteration of the equation system until the error relative to the gas pressure of all partial pressures was below -6 dex. The computations were then performed and tabulated in a [P,T]-plane encompassing largely the conditions prevailing in low mass stars and brown dwarfs (P = -4 to 12 and T = 15000 to 10K), using a solar mix except for lithium (meteoretic abundance, same source). The CE tables were then interpolated in the construction of the model atmospheres.

The CE therefore accounts, self-consistently, for the depletion of refractory elements as a function of the gas temperature and pressure conditions in the model atmospheres. However, it should be clear that thermodynamic equilibrium studies only tell us what can be formed, not what is formed. And the results are only as certain as the JANAF equilibrium constants on which they are based. In favor of CE, note however that , who used thermodynamics, were able to explain the abundance patterns of various trace elements dissolved in carbide stardust. We therefore feel confident that our CE calculations allow us at least to reproduce, in average, adequately the limiting thermal and spectroscopic properties of brown dwarfs. However we do not claim that this CE calculation predicts exactly the distribution of dust species in brown dwarfs atmospheres. Gravitational settling effects would certainly change this distribution. We note in passing that our main results concur with both those of and . This consistency between independent CE works is reassuring.

In this work, contrary to recent calculations by , we have not attempted to handle the effects of gravitational settling (i.e. diffusion of the grains to lower atmospheric layers). We do not account for elemental abundance depletion resulting from dust grain settling. This process is likely important in the uppermost layers of brown dwarf atmospheres, and would tend to deplete these layers of their refractory elements and dust grains. However, the error introduced by this omission on the models presented in this paper is small since these represent limiting cases with non-existent and complete settling, where the dust opacity has been ignored altogether to recreate the latter case. The available abundance of refractory elements involved in dust formation can however be slightly overestimated. The complete treatment of gravitational settling goes beyond a simple parametrization of the problem, and involves solving the diffusion of the dust as a function of the characteristic timescale of several important processes such as the sedimentation, coagulation, condensation and convective mixing of the dust. This work is, however, under development and we will present our findings in a separate publication.

Since the predictions of CE calculations have been described in detail by and , we do not deem necessary to develop this here again. Yet the completeness of the grain species sample included here (within the limits of the CE approximation and JANAF data) provides an opportunity to explore some of the effects of condensation upon the composition of late-type dwarf stars and brown dwarfs atmospheres. In the atmospheres of brown dwarfs, most of the hydrogen is locked in H₂, most of the oxygen is in CO, H₂O and SiO, and most of the carbon is in CO and CH₄. The species responsible for the strong optical to near-infrared (0.4 to 1.1 $\mu$m) opacities in M dwarf stars and young brown dwarfs are relatively trace species much less abundant then CO or H₂O, which have large opacity cross-sections per molecule. The relative abundance of those species are summarized in Figure  and 2 which illustrate the nature and progression of the condensation layers into deeper layers of the photosphere as ${\rm T}_{\rm eff}$ decreases. At a ${\rm T}_{\rm eff}\ = 2600\,$K which is typical of the young Pleiades brown dwarfs Teide1 and Calar3 , the clouds barely touch the top layers of the photosphere which is located between $\tau_{1.2{\mu}m} = 10^{-4}$ to 1 depending on the spectral range considered. As can be seen from the inner to outer atmospheric regions (right to left on the plots), the first species to condense at T $\approx 2000$K is ZrO₂, followed by corundum (Al₂O₃) at T $\approx 1800$K. We clearly identify the perovskite CaTiO₃ as the source of depletion of TiO, the principle optical absorber in these atmospheres. However, the depletion occurs in this model only above the photosphere and should leave the spectra relatively unaffected. Other stable species to appear at T<1600K are MgAl₂O₄, CaSiO₃, Ca₂SiO₄, Ca₂Al₂SiO₇, Ca₂MgSi₂O₇, and CaMgSi₂O₆, as well as Ti₄O₇ and Ti₂O₃. These grains all compete with the formation of CaTiO₃ and corundum, and form an intricate layer of clouds just above the photosphere. Note that, contrary to the reports by , corundum is not the most abundant grain species and even disappears in central regions of the clouds.

The situation complicates rapidly as ${\rm T}_{\rm eff}$ decreases. Figure  shows how the clouds have already invaded most of the photosphere in brown dwarfs of about 1800K typical of field brown dwarfs such as GD165B , Kelu1 or the DENIS objects . Dozens of new grain species including iron, enstatite (MgSiO₃) and forsterite (Mg₂SiO₄) are now present. The photospheric gas phase abundances of TiO, FeH, and CaH (not shown) are now strongly depleted. This is reflected by the gradual disappearance of these features in the latest-type M dwarfs and brown dwarfs, a behavior which is already apparent from the observed spectra of brown dwarf candidates BRI0021, GD165B and Kelu1. The VO abundances seem, on the other hand, much less depleted by the condensation of VO and V₂O₄ occurring only in the upper photosphere. And other compounds of less-reactive elements such as Li, K, Rb, Cs, and CrH are left relatively unaffected, favoring the detection of their features in these objects.

Between ${\rm T}_{\rm eff}\ = 1800$ and $1000\,$K, methane (CH₄) gradually forms at the expense of CO. The likelihood of detecting methane lines in the spectra of cool brown dwarfs depends therefore on the height in the atmosphere where this transition regime occurs, and depends upon ${\rm T}_{\rm eff}$, gravity, and dust opacity conditions such as gravitational settling, rotation, winds, etc.

Although the clouds appear to persist in Figures and 2 out to the outer edge of the photosphere in our coolest models, this only reflects the omission, mentioned above, of the gravitational settling of the grains. Clouds form more likely in thin decks above the deepest condensation layer in brown dwarfs .

The principle impact of condensation on the photospheres and spectra of cool dwarf is a gradual depletion of their refractory elements, especially zirconium, titanium, silicon, calcium, magnesium, aluminum, iron and nickel. Clearly, it is crucial for the balance of the opacities in the models to account for the leading grain species in the chemical equilibrium. Partially accounting for condensation leads to errors of several orders of magnitudes in the model opacities and predicted fluxes. See for a comparison between existing dusty models. To fully understand the spectroscopic and photometric properties of brown dwarfs, one must also consider the optical and radiative properties of dust grains.

for a comparison between existing dusty models. To fully understand the spectroscopic and photometric properties of brown dwarfs, one must also consider the optical and radiative properties of dust grains.