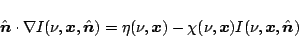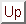

Next: The operator splitting method
Up: Method
Previous: Framework
The static radiative transfer equation in 3-D may be written
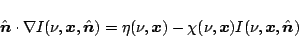 |
(1) |
where
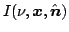 is the specific intensity at frequency
is the specific intensity at frequency
 , position
, position  , in the direction
, in the direction  ,
,
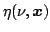 is the emissivity at frequency
is the emissivity at frequency
 and position
and position  , and
, and
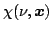 is the total
extinction at frequency
is the total
extinction at frequency
 and position
and position  . The source function
. The source function
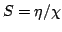 . Here, we will work in the steady-state so that
. Here, we will work in the steady-state so that
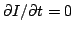 , and in Cartesian coordinates so
the
, and in Cartesian coordinates so
the
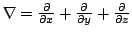 and the direction
and the direction  is
defined by two angles
is
defined by two angles  at the position
at the position  .
.
Peter Hauschildt
2006-01-09