

Next: The Rate Operator
Up: The Problem
Previous: Numerical Considerations
In order to solve Eq. 1, the emissivity 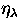 must be known, but
must be known, but 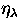 depends on the NLTE level
populations and therefore the NLTE rate equations must be solved
simultaneously with Eq. 1. This is further complicated by
the fact that the NLTE rate equations depend on the radiation field itself.
The NLTE rate equations have the form [11]
depends on the NLTE level
populations and therefore the NLTE rate equations must be solved
simultaneously with Eq. 1. This is further complicated by
the fact that the NLTE rate equations depend on the radiation field itself.
The NLTE rate equations have the form [11]
In Eq. 16, ni is
the actual, non-LTE population density of a level i
and the symbol ni* denotes the so-called LTE population density
of the level i, which is given by
Here 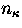 denotes the actual, i.e., non-LTE,
population density of the ground
state of the next higher ionization stage of the same element;
gi and
denotes the actual, i.e., non-LTE,
population density of the ground
state of the next higher ionization stage of the same element;
gi and 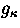 are
the statistical weights of the levels i and
are
the statistical weights of the levels i and 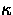 , respectively.
In Eq. 17, Ei is the excitation energy of the level i and
, respectively.
In Eq. 17, Ei is the excitation energy of the level i and
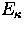 denotes the ionization energy from the ground state to
the corresponding ground state of the next higher ionization stage.
The actual, non-LTE electron density is given by ne. The system of
rate equations is closed by the conservation equations for the nuclei and the
charge conservation equation (cf. Ref. [11]).
denotes the ionization energy from the ground state to
the corresponding ground state of the next higher ionization stage.
The actual, non-LTE electron density is given by ne. The system of
rate equations is closed by the conservation equations for the nuclei and the
charge conservation equation (cf. Ref. [11]).
The sums in Eq. 16 extend only over the levels that are
included in our model atoms; for example, in singly ionized iron our
model atom
consists of 675 energy levels [3]. The weaker radiative
transitions are treated as LTE background opacity (see
Refs. [2,3]).
The rate coefficients for radiative and collisional transitions between
two levels
i and j (including transitions from and to the continuum, see below)
are given by
Rij and Cij, respectively.
In our notation, the upward (absorption) radiative rate coefficients Rij
(i<j)
are given by
whereas the downward (emission) radiative rate coefficients Rji
(i<j) are
given by
Here, J is the mean intensity, T the electron temperature, h and
c and Planck's constant and the speed of light, respectively.
For the purposes of this paper, we assume that
cross section 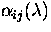 of the transition
of the transition 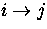 at the
wavelength
at the
wavelength 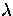 is known for both line and continuum transitions
and that it is the same for both absorption and emission processes
(complete redistribution).
is known for both line and continuum transitions
and that it is the same for both absorption and emission processes
(complete redistribution).
Not all atomic processes fit neatly into the above scheme where the
rates are in detailed balance. Non-thermal ionization by fast
electrons, K-capture, Auger emission, and two-photon decay are
important in various stages of the evolution of novae and
supernovae. They can be included in the above formulation with
reasonable approximations, however.


Next: The Rate Operator
Up: The Problem
Previous: Numerical Considerations
Peter H. Hauschildt
8/20/1998
![]() must be known, but
must be known, but ![]() depends on the NLTE level
populations and therefore the NLTE rate equations must be solved
simultaneously with Eq. 1. This is further complicated by
the fact that the NLTE rate equations depend on the radiation field itself.
The NLTE rate equations have the form [11]
depends on the NLTE level
populations and therefore the NLTE rate equations must be solved
simultaneously with Eq. 1. This is further complicated by
the fact that the NLTE rate equations depend on the radiation field itself.
The NLTE rate equations have the form [11]