The equation of radiative transfer (RTE) in spherical symmetry for moving media has been solved with a number of different methods, e.g. Monte Carlo calculations [12,13,14], Sobolev methods [15], the tangent ray method [16], and the DOME method [17]. Only the tangent ray and the DOME method have been used to solve the RTE for very fast expanding shells (e.g. supernovae or novae) including the necessary special relativistic terms. Both methods need relatively large amounts of CPU time to compute the radiation field, mainly because of the need for matrix inversions (tangent ray method) or matrix diagonalization (DOME), which make both of them impractical for use within radiation-hydrodynamic studies of nova or supernova explosions. It has been shown [18] that the special relativistic terms in the RTE can be very important, even in the optically thick regions of expanding shells, and lead to results different than from the simpler approach which simply neglects the relativistic terms.
Recently, iterative methods for the solution of the RTE have been developed,
based on the philosophy of operator perturbation [19,20].
Following these ideas, different approximate ![]() -operators for this
``accelerated
-operators for this
``accelerated ![]() -iteration'' (ALI) method have been used successfully
[21,22,23] and have been applied to the construction of
non-LTE, radiative equilibrium models of stellar atmospheres [23].
-iteration'' (ALI) method have been used successfully
[21,22,23] and have been applied to the construction of
non-LTE, radiative equilibrium models of stellar atmospheres [23].
We describe the use of the short-characteristic method [21,24] to
obtain the formal solution of the special relativistic, spherically symmetric
radiative transfer equation (SSRTE) along its characteristic rays and then use
a band-diagonal approximation to the discretized ![]() -operator
[1,24,25] as our choice of the approximate
-operator
[1,24,25] as our choice of the approximate ![]() -operator.
This method can be implemented very efficiently to obtain an accurate solution
of the SSRTE for continuum and line transfer problems using only modest amounts
of computer resources.
-operator.
This method can be implemented very efficiently to obtain an accurate solution
of the SSRTE for continuum and line transfer problems using only modest amounts
of computer resources.
The co-moving frame radiative transfer equation for spherically symmetric flows can be written as [26]:
![]() is the velocity in units of the speed of light, c; and
is the velocity in units of the speed of light, c; and
![]() is the usual Lorentz factor.
Equation 1 is a integro-differential equation, since the
emissivity
is the usual Lorentz factor.
Equation 1 is a integro-differential equation, since the
emissivity ![]() contains J_
contains J_![]() , the zeroth angular moment of
I_
, the zeroth angular moment of
I_![]() :
:

Switching from frequency to wavelength (Eq. 1 is presented
in Ref. [1] in wavelength),
the mean intensity ![]() is obtained from the source function
is obtained from the source function
![]() by a formal solution of the RTE which is symbolically written
using the
by a formal solution of the RTE which is symbolically written
using the ![]() -operator
-operator ![]() as
as
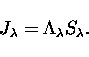 |
(1) |
The ![]() -iteration method, i.e. to solve Eq. 4 by a fixed-point
iteration scheme of the form
-iteration method, i.e. to solve Eq. 4 by a fixed-point
iteration scheme of the form