


Next: About this document ...
Parallel Supercomputing In Stellar Atmosphere Simulations
Peter H. Hauschildt
Department of Physics & Astronomy
and
Center for Simulational Physics
The University of Georgia
Athens, GA 30602
in collaboration with
E. Baron (Univ. of OK)
F. Allard (WSU & CNRS/Lyon)
D. Lowenthal (UGA)
Overview
- 1.
- Motivation
- 2.
- The Computational Problem
- 3.
- Solution through parallelization
- 4.
- Parallel algorithms
- 5.
- Conclusions & The Future
Motivation
- astrophysical information through spectroscopy
- velocities
- temperatures
- densities
- element abundances
- luminosities
- detailed modeling required to extract physical data
from observed spectra
- follow radiative transfer
of photons of all wavelengths through the atmosphere in great detail
-
 synthesize spectrum to compare to observations
synthesize spectrum to compare to observations
- basic physical model
- spherical shell
- static (stars) or expanding (novae, winds, SNe)
- hydrostatic or hydrodynamical equilibrium
- central source provides energy
- Constraint equations:
- energy conservation
 temperature structure
temperature structure
- momentum conservation
 pressure & velocity structure
pressure & velocity structure
- ``Auxiliary'' equations:
Radiative Transfer
true cm
Assumptions:
- spherical symmetry,
- time independence (
 ),
),
- full special relativistic treatment in the
Lagrangian frame.
Spherically symmetric, special relativistic equation
of radiative transfer
- partial integro-differential equation,
- telegrapher's equation: boundary value problem in r
and initial value problem in
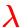 (certain restrictions apply)
(certain restrictions apply)
The equation of radiative transfer
true cm

with
and
-
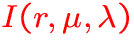 : specific intensity scaled by r2,
: specific intensity scaled by r2,
- r: radial coordinate,
-
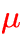 : cosine of the direction angle,
: cosine of the direction angle, 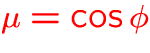
- v: velocity,
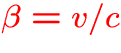 ,
, 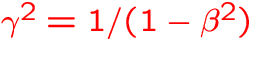 ,
, -
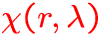 :
extinction coefficient,
:
extinction coefficient, 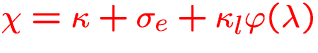
-
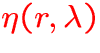 : emissivity.
: emissivity.
Example for 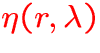
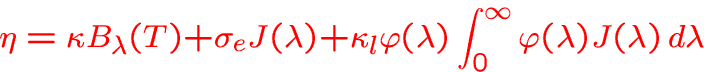
with
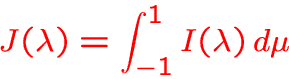
-
 : thermal emission
: thermal emission
-
 : electron scattering
: electron scattering
-
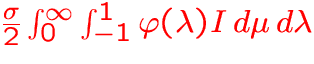 :spectral line emissivity
:spectral line emissivity
Numerical solution:
- Basic idea: discretize
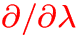 and
treat the boundary value problem for each wavelength individually,
and
treat the boundary value problem for each wavelength individually,
- Operator splitting (OS) method
- solve along characteristics of the RTE
- iterative method:
- piecewise parabolic ansatz to calculate I for given J
- iterate to self-consistent solution for J
- eigenvalues of iteration matrix close to unity
 use operator splitting to reduce eigenvalues of amplification
matrix
use operator splitting to reduce eigenvalues of amplification
matrix
Statistical Equilibrium Equations
true cm
 Line and continuum scattering
prevents the use of the
Line and continuum scattering
prevents the use of the 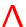 -iteration for the
solution of the rate equations!
-iteration for the
solution of the rate equations!
Solution of the statistical equilibrium equations:
true cm
Operator Splitting method:
- define a ``rate operator'' in analogy to the
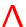 -operator:
-operator:
Rij = [Rij][n]
- define an ``approximate rate operator''
![$\ifmmode{[R_{ij}^*]}\else\hbox{$[R_{ij}^*]$}\fi$](img22.gif) and
write the iteration scheme in the form:
and
write the iteration scheme in the form:
![\begin{displaymath}
R_{ij} = \ifmmode{[R_{ij}^*]}\else\hbox{$[R_{ij}^*]$}\fi[n_{...
...ode{[R_{ij}^*]}\else\hbox{$[R_{ij}^*]$}\fi\right) [n_{\rm old}]\end{displaymath}](img23.gif)
=0pt
The Computational Problem
- 1.
- input data size
- number of atomic/ionic spectral lines:
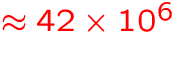
 GB
GB
- number of diatomic molecular lines:
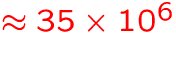
 GB
GB
- number of hot water vapor lines:
- 2.
- sep=0pt
- before 1994:
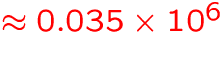
- 1994:
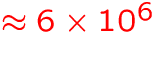
 GB
GB
- 1997:

 GB
GB
- expected 1998:
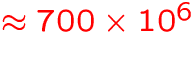
 GB
GB
- all lines need to be accessed in a line selection
procedure
- line selection creates sub-lists that can be as large as
the original list
-
 poses a significant data handling problem!
poses a significant data handling problem!
- 3.
- memory/IO requirements
- line lists too large for memory
 scratch files & block algorithm
scratch files & block algorithm
 trade memory for IO bandwidth
trade memory for IO bandwidth
- number of individual energy levels:


 MB
MB
- number of individual transitions:
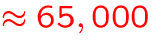

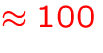 MB
MB
- EOS data storage
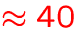 MB
MB
- auxiliary storage
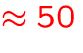 MB
MB
-
 total memory requirement
total memory requirement  MB
MB
- number of individual energy levels and transitions will increase
dramatically
 memory requirements
memory requirements 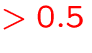 GB
GB
- 4.
- (serial) CPU time
- small for each individual point on the wavelength grid:
 msec
msec
- number of wavelength points for radiative transfer:
30,000-300,000 (can be >106)
-
 up to 30,000 sec to ``sweep'' once through all wavelength points
up to 30,000 sec to ``sweep'' once through all wavelength points
- typically,
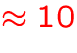 iterations (sweeps) are required to
obtain an equilibrium model
iterations (sweeps) are required to
obtain an equilibrium model
-
 CPU days
CPU days
- there are, literally, 100's of models in a typical grid ...
Solution through parallelization
- 1.
- portability issues
- large number of simulations
- complex code (verification on several different architectures)
- need to be able to run efficiently on different parallel supercomputers
-
 Fortran 90 & MPI
Fortran 90 & MPI
- available on all major platforms
- public domain implementation MPICH
- 2.
- memory issues
- MPI available on distributed memory systems
- large aggregate memory of distributed memory machines
- allows reduction of memory requirements per node
-
 larger model calculations possible!
larger model calculations possible!
- 3.
- IO issues
- parallel filesystems allow file partitioning
- results in higher IO throughput
- parallel code: each node needs to read only part of the data
 IO reduction on per-node basis
IO reduction on per-node basis
- but sometimes better scalability means more IO
- 4.
- scalability issues
- allows more efficient usage of multiple CPUs
- reduces wall-clock time for typical simulations
- depends very often on type of models:
some simulations (stars) allow algorithms that scale very well, but
some simulations (novae, SNe) do not
-
 implement several algorithms that can be selected at run-time
to obtain ``best'' overall performance while making simulations feasible!
implement several algorithms that can be selected at run-time
to obtain ``best'' overall performance while making simulations feasible!
Parallel algorithms
- 1.
- The PHOENIX code
- 2.
- Spectral line selection
- serial version can take 3h for the large line lists!
- 3 separate line lists
 task parallelism
task parallelism
- data parallelism: use client-server model
- clients: select lines in assigned chunks of the line list files
- server: collects data and creates sorted sub-list files
- potentially reduces time proportional to the number of client nodes
- creates large message traffic
- 3.
- Spectral line opacity calculations
- 4.
- Radiative transfer
- characteristic ``rays'' are independent
 parallelize ``formal solution'' part of iteration
parallelize ``formal solution'' part of iteration
- problem: number of mesh points along each characteristic is different
-
 need to balance load by distributing sets of characteristics to nodes
need to balance load by distributing sets of characteristics to nodes
- scalability low because of load-balance and communication overhead
problems
- 5.
- Parallelizing the wavelength loop

Conclusions & The Future
- parallelization of PHOENIX allows physically more detailed
models
- decrease in wall-clock time per model is substantial for many
types of simulations
- coding effort to implement MPI calls relatively small
(about 7400 lines)
- logic for algorithm selection and load balancing fairly complex
- parallel version of PHOENIX is regularly used in production
- depending on simulation type we use between 4 and 64 nodes (single CPU)
In the Future
- parallel asynchronous IO (MPI-2)
- radiative transfer for arbitrary velocity fields (requires 70-700 GB
of memory/disk space)
- time dependence
- 3D RT in the Lagrangian frame for optically thick moving configurations



Next: About this document ...
Peter H. Hauschildt
4/27/1999
 temperature structure
temperature structure
 pressure & velocity structure
pressure & velocity structure
 special relativistic form
special relativistic form
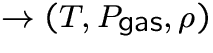 relation
relation
 need to include many ions
need to include many ions
 need to include 100's of molecules & dust species
need to include 100's of molecules & dust species
 relate the population of each energy level to non-local radiation
field and to collisional processes
relate the population of each energy level to non-local radiation
field and to collisional processes
 must be solved together
must be solved together
 statistical equations are inherently non-local
statistical equations are inherently non-local
 account for blocking of photons & synthesize spectral features
account for blocking of photons & synthesize spectral features
 spectral analysis
spectral analysis
 ),
),

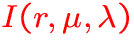 : specific intensity scaled by r2,
: specific intensity scaled by r2,
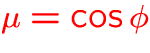
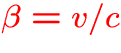 ,
, 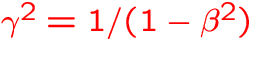 ,
,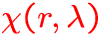 :
extinction coefficient,
:
extinction coefficient, 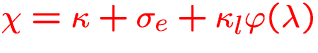
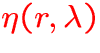 : emissivity.
: emissivity.
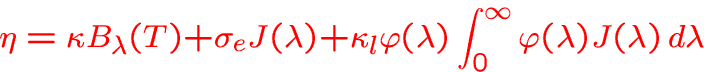
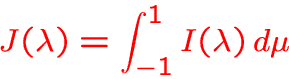
 : thermal emission
: thermal emission
 : electron scattering
: electron scattering
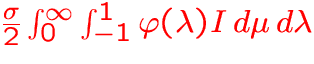 :spectral line emissivity
:spectral line emissivity
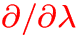 and
treat the boundary value problem for each wavelength individually,
and
treat the boundary value problem for each wavelength individually,
![$\ifmmode{[R_{ij}^*]}\else\hbox{$[R_{ij}^*]$}\fi$](img22.gif) and
write the iteration scheme in the form:
and
write the iteration scheme in the form:
![\begin{displaymath}
R_{ij} = \ifmmode{[R_{ij}^*]}\else\hbox{$[R_{ij}^*]$}\fi[n_{...
...ode{[R_{ij}^*]}\else\hbox{$[R_{ij}^*]$}\fi\right) [n_{\rm old}]\end{displaymath}](img23.gif)
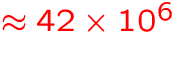
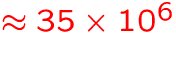
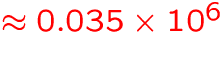
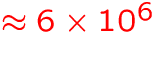

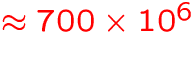

 MB
MB
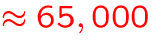
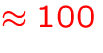 MB
MB
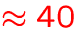 MB
MB
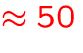 MB
MB
 MB
MB
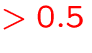 GB
GB
 msec
msec
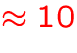 iterations (sweeps) are required to
obtain an equilibrium model
iterations (sweeps) are required to
obtain an equilibrium model
 CPU days
CPU days
