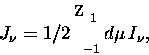

Next: Machines used for testing
Up: Parallel Implementation of the
Previous: Introduction
The co-moving frame radiative transfer equation for spherically
symmetric flows can be written
as :
We set c=1;  is the velocity; and
is the velocity; and
 is the usual Lorentz factor.
Equation
is the usual Lorentz factor.
Equation ![[*]](cross_ref_motif.gif) is a integro-differential equation, since the
emissivity
is a integro-differential equation, since the
emissivity 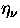 contains J_
contains J_ , the zeroth angular moment of
I_
, the zeroth angular moment of
I_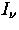 :
:
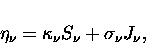
and
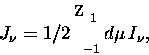
where  is the source function,
is the source function,  is the absorption
opacity, and
is the absorption
opacity, and  is the scattering opacity.
With
the assumption of time-independence
is the scattering opacity.
With
the assumption of time-independence  and a monotonic velocity field Eq. 1 becomes a boundary-value problem in
the spatial coordinate and an initial value problem in the frequency
or wavelength coordinate. The equation can be written in operator form
as:
and a monotonic velocity field Eq. 1 becomes a boundary-value problem in
the spatial coordinate and an initial value problem in the frequency
or wavelength coordinate. The equation can be written in operator form
as:
where 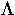 is the lambda-operator.
is the lambda-operator.
Peter H. Hauschildt
4/27/1999
![[*]](cross_ref_motif.gif) is a integro-differential equation, since the
emissivity
is a integro-differential equation, since the
emissivity ![]() is the velocity; and
is the velocity; and
![]() is the usual Lorentz factor.
Equation
is the usual Lorentz factor.
Equation ![[*]](cross_ref_motif.gif) is a integro-differential equation, since the
emissivity
is a integro-differential equation, since the
emissivity ![]() contains J_
contains J_![]() , the zeroth angular moment of
I_
, the zeroth angular moment of
I_![]() :
:
![]()