Temperature correction procedure

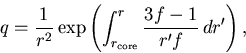
We iterate for the temperature structure of the atmosphere using a generalization of the Unsöld-Lucy temperature correction scheme to spherical geometry and NLTE model calculations. This has proven to work very well even in extreme NLTE cases such as nova and supernova atmospheres. The temperature correction procedure also requires virtually no memory and CPU time overhead. The Unsöld-Lucy correction scheme , uses the global constraint equation of energy conservation to find corrections to the temperature that will fulfill energy conservation better than the previous estimate. We have found it to be more stable than a Newton-Raphson linearization scheme and it allows us to separate the temperature corrections from the statistical equations. The latter property is extremely useful in NLTE calculations where it allows us to use a nested iteration scheme for the energy conservation and the statistical equilibrium equations. This significantly increases numerical stability and allows us to use much larger model atoms than more conventional methods.

To derive the Unsöld-Lucy correction, one uses the fact that the ratios of the wavelength averaged absorption and extinction coefficients

(where B,J,F denote the wavelength integrated Planck function, mean intensity and radiation flux, respectively) depend much less on values of the independent variables than do the averages themselves.

Dropping terms of order (v/c), one can then use the angular moments of the radiative transfer equation to show that in order to obtain radiation equilibrium B should be corrected by an amount

where $H\equiv F/4\pi$, $H_0(\tau)$ is the value of the target luminosity at that particular depth point (variable due to the velocity terms in comoving frame radiative transfer calculations and non-mechanical energy sources, the total observed luminosity H₀(0) is an input parameter), Here, q is the ``sphericity factor'' given by

$$q = \frac{1}{r^2}\exp\left(\int_{r_{\rm core}}^r\frac{3f - 1}{r'f}\, dr'\right),$$

where $r_{\rm core}$ is the inner radius of the atmosphere, R is the total radius, $f(\t)=K(\t)/J(\t)$ is the ``Eddington factor'', and $K=\int \mu^2 I \, d\mu$ is the second angular moment of the mean intensity. $\dot S$describes all additional sources of energy such as mechanical energy supplied by winds or non-thermal ionization due to $\gamma$-ray deposition.

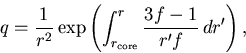
The first term in Eq.  corresponds simply to a $\Lambda$ iteration term and will thus provide temperature corrections that are smaller than required in the inner parts of the atmosphere, but will be accurate in the outer, optically thin parts. The second term of Eq. 5, however, is the dominant term in the inner parts of the atmosphere. It provides a very good approximation to the temperature corrections $\Delta T$ deep inside the atmosphere. Following , we have found that it is sometimes better to modify this general scheme by excluding the contributions of extremely strong lines in the opacity averages used for the calculations of $\Delta T$ because they tend to dominate the average opacity but do not contribute as much to the total error in the energy conservation constraint.

, we have found that it is sometimes better to modify this general scheme by excluding the contributions of extremely strong lines in the opacity averages used for the calculations of $\Delta T$ because they tend to dominate the average opacity but do not contribute as much to the total error in the energy conservation constraint.