Bibliography

**Figure 1:** The mean intensity and the component of the radiation flux at $\ifmmode{\tau_{\rm std}}\else\hbox{$\tau_{\rm std}$}\fi =0$ as function of wavelength. The symbols are the comparison results with the 1D solver, the full lines the results from the 3D PBC solution. The results are for $\epsilon _l=1$ and constant temperatures.

**Figure 2:** The mean intensity and the component of the radiation flux at $\ifmmode{\tau_{\rm std}}\else\hbox{$\tau_{\rm std}$}\fi =0$ as function of wavelength. The symbols are the comparison results with the 1D solver, the full lines the results from the 3D PBC solution. The results are for $\epsilon _l=10^{-2}$ and constant temperatures.

**Figure 3:** The mean intensity and the component of the radiation flux at $\ifmmode{\tau_{\rm std}}\else\hbox{$\tau_{\rm std}$}\fi =0$ as function of wavelength. The symbols are the comparison results with the 1D solver, the full lines the results from the 3D PBC solution. The results are for $\epsilon _l=10^{-4}$ and constant temperatures.

**Figure 4:** The mean intensity and the component of the radiation flux at $\ifmmode{\tau_{\rm std}}\else\hbox{$\tau_{\rm std}$}\fi =0$ as function of wavelength. The symbols are the comparison results with the 1D solver, the full lines the results from the 3D PBC solution. The results are for $\epsilon _l=10^{-8}$ and constant temperatures.

**Figure 5:** Convergence rates of the 3D transfer for line transfer with plane-parallel test structures (label 'PP') and the 3D hydro structure (label 'hydro'). For comparison, the convergence of the $\Lambda$ iteration for plane-parallel continuum transfer is also shown.

Figure 6: Visualization of the results for continuum 3D radiation transfer for $\epsilon _c=1$ (left panel) and $10^{-2}$ (right panel). The images are intensities in the directions $\phi=25\deg$ and $\theta=0\deg$ (top row) and $\theta=40\deg$ (bottom row). An observer would only see the left face of the cube (inside the indicated area), the other sides of the cube are shown for clarity and are actually invisible due to the periodic boundary conditions. The scaling of the intensities is the same within each column but different for the left and right columns.

$\includegraphics[width=0.95\hsize,angle=0]{10239f6a.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f6b.eps}$

$\includegraphics[width=0.95\hsize,angle=0]{10239f6c.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f6d.eps}$

Figure: Same as Fig. 6, but for $\theta=60\deg$ (top row) and 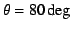$\theta=80\deg$ (bottom row). The scaling of the intensities is as in Fig. 6. The effect of limb darkening is clearly visible in this figure.

$\includegraphics[width=0.95\hsize,angle=0]{10239f7a.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f7b.eps}$

$\includegraphics[width=0.95\hsize,angle=0]{10239f7c.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f7d.eps}$

Figure: Limb darkening (left panel) and contrast $\sqrt{\langle(I-\langle I\rangle )^2\rangle )}/\langle I\rangle$ for 3D continuum transfer with the hydro structure.

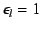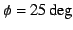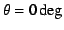Figure 9: Visualization of the results for the line 3D radiation transfer with $\epsilon _l=1$ . The images are intensities in the directions $\phi=25\deg$ and $\theta=0\deg$ . The top left panel is the image in the continuum, the top right panel the image at the line center, the bottom left panel the image in the line wing, the bottom right panel is a composite image.

$\includegraphics[width=0.95\hsize,angle=0]{10239f9a.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f9b.eps}$

$\includegraphics[width=0.95\hsize,angle=0]{10239f9c.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f9d.eps}$

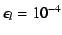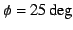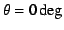Figure 10: Visualization of the results for the line 3D radiation transfer with $\epsilon _l=10^{-4}$ . The images are intensities in the directions $\phi=25\deg$ and $\theta=0\deg$ . The top left panel is the image in the continuum, the top right panel the image at the line center, the bottom left panel the image in the line wing, the bottom right panel is a composite image.

$\includegraphics[width=0.95\hsize,angle=0]{10239f10a.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f10b.eps}$

$\includegraphics[width=0.95\hsize,angle=0]{10239f10c.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f10d.eps}$

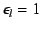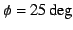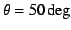Figure 11: Visualization of the results for the line 3D radiation transfer with $\epsilon _l=1$ . The images are intensities in the directions $\phi=25\deg$ and $\theta=50\deg$ . The top left panel is the image in the continuum, the top right panel the image at the line center, the bottom left panel the image in the line wing, the bottom right panel is a composite image.

$\includegraphics[width=0.95\hsize,angle=0]{10239f11a.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f11b.eps}$

$\includegraphics[width=0.95\hsize,angle=0]{10239f11c.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f11d.eps}$

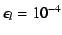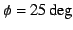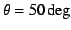Figure 12: Visualization of the results for the line 3D radiation transfer with $\epsilon _l=10^{-4}$ . The images are intensities in the directions $\phi=25\deg$ and $\theta=50\deg$ . The top left panel is the image in the continuum, the top right panel the image at the line center, the bottom left panel the image in the line wing, the bottom right panel is a composite image.

$\includegraphics[width=0.95\hsize,angle=0]{10239f12a.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f12b.eps}$

$\includegraphics[width=0.95\hsize,angle=0]{10239f12c.eps}$ $\includegraphics[width=0.95\hsize,angle=0]{10239f12d.eps}$